COSC 3402 Artificial Intelligence

<<< Situation Calculus

Neural Networks (NN)

A non-symbolic approach to knowledge representation.

Artificial Neuron:
     i1--w1-->|----\
     i2--w2-->|     \
->        ...>|  f   >------> f(net)
i    ik--wk-->|     /
     -------->|----/         (f = activation function)
      Bias 
       (Constant Value)
    
Domain for inputs (and outputs):
(1) R
(2) [0,1]
(3) [-1,1]
(4) {0,1}

w is the weight of input, so:
i1.w1 + i2.w2 + ... + ik.wk + w.bias = net
i.e.
net = Σ(1,k,i.w) + w.bias

The values of input and output must be in the same domain

Example:
         |- 1: net >= 0
f(net) = |
         |- 0: net < 0
     
net = x.1 + y.1 - 2 = x + y - 2

     x -(+1)->|----\
              |     \
->            |  f   >------> f(net)
i    y -(+1)->|     /
     1 -(-2)->|----/ 
     D = {0,1}
     
     x | y | net | f(net)
    ---+---+-----+--------
     0 | 0 | -2  |  0
     1 | 0 | -1  |  0          (logical '^')
     0 | 1 | -1  |  0
     1 | 1 |  0  |  1

What if bias is replaced with -1?

Neural Networks:
[1]----+-|\
[2]--+-|-| |----------|\
[3]+-|-|-|/           | \
   | | +----|\        | /  (inputs can go to every neuron)
   | +------| |-------|/
   +--------|/

NN as layers of neurons

• Layers of neurons where each layer can only send information to the next layer
• The last layer is the output layer.
• All other layers are hidden layers.
• All neorons in the same layer have the same function.
• net_ij indicates the net in neuron j in layer i.

Perceptron Architecture: Single layer NN

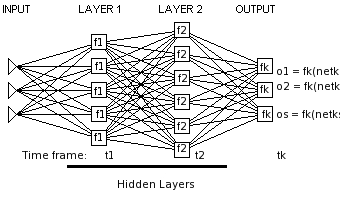
Neural networks can be simplified so there is only the output layer. Since these neurons don't depend on eachother and they all have the same function, we can only keep one.

Example
Recognize pattern A
Solution: use supervised training (of a perceptron)
-- We want the perceptron to return YES if the input is "A"
      and NO otherwise.

Supervised training

+----------------------------------------------------+
| Non-A characters         +--------------+          |
|                          | 'A'characters|          |
|               +-----------------+       |          |
|               |          |      |       |          |
|               | Finite   +------|-------+          |
|               | Training Set    |                  |
|               +-----------------+                  | D - domain
+----------------------------------------------------+ of objects

Objective: after the training, the NN will, with high probability, 
classify all the characters in the domain correctly.

Training set T:
    T = {(i1,an1),(i2,an2),...,(ik,ank)}
        - if all inputs are correct, the training is done
        - Other wise we repeat until they are all correct

How to adjust weights? For input i, we compare an with f(net)
delta = an - f(net)
w_l := w_l + C.delta.i_l c < 1 learning note

PERCEPTRON LEARNING ALGORITHM

INPUT:  initial weights w1,...,wk
        training set T = {(i1,an1),(i2,an2),...,(ik,ank)}
        learning note  0 < C < 1

OUTPUT: modified w1,...,wk

METHOD:
    change = true
    while change do
        change = false
        for every training pair (is, ans) do  /* is = (is1,...,isk) */
            delta = (ank - f(netk)) for input ik
            if delta /= 0
                for every input weight wj do
                    wj := wj + C.delta.isj
                w = w + C.delta
                change = true
    output w1,...,wk

A problem (in 2D) is any set of points on the plain.

Definition: A problem P is Linearly Separable if there exists a line l such that all the points in P are below or above l. I.E. l seperates all the positive instances from all the negative instances of the problem.

^
|\
|+\ -
|  \  -
|+ +\-
| +  \   -
+-----\-------------->

Fact: Perceptron can only learn linearly seperable problems.

Example (see the previous example)
Negative Example:
^       -     -
|    - #########    -
|  -   #+ +  + # -
|   -  # +  +  #  -
|   -  #+  +  +#  -
|      #########   -
|  -   -     -   -
+-------------------->
The problem above can not be learned by a perceptron.

Back Propagation NN (BPNN)

Note: All activation functions in BPNN are continuous. Typically:
f(x) = 1 / ( 1 + e^-x )

Let in be the input to BPNN and let out = (out₁,..., out_n) be the output. If out = an (note: (in,an) is from training set), there is no need to correct weights.

Suppose that an /= out. Let N be an output neuron such that out_N /= an_N.

  i1--w1-->|\
  i2--w2-->| \
       ...>|  >------> f(net) = outN /= anN
  ik--wk-->| /
  1 --w--->|/ 

Let us consider the net_N value.

Compute error term Δ_N

for N:

ΔN = ( anN - outN ) . f'(net)

(Note that f'(net) returns (and sets Δ to) zero where f(net) is flat.)

New weights: Wj = Wj + C.Δ_N.i_j

Let us consider a neuron M from 2nd lost layer.

  i1--w1-->|\   / V1  Δ1
  i2--w2-->| \ /
       ...>|M >--- V2  Δ2 /= 0
  ik--wk-->| / \
  1 --w--->|/   \ V3  Δ3
               outM = f(netM)

M computes its error term:
    ΔM = Σ(1,n,V.Δ) . f'(netM)

Correct weights: Wj = Wj + C.Δ_M.i_j

           +--------+                   \
  i1--w1-->|        |-Δ1-> out1   an11  |
  i2--w2-->|        |                    |
       ...>|        |-Δ2-> out2   an12   > an1
  in--wn-->|        | ...                |
  1 --w--->|        |-Δk-> outk   an1k  |
           +--------+                   /

T:(i₁, an₁), ..., (i_t, an_t)

Δ = l=1Σt j=1Σk Δj2

^ Δ
| .
|   .
|     .       .   .
|       .   .   .
|         .
+-------------------->

Termination condition for the BPNN is the first minimum for Δ

GeneticAlgorithms >>>